В правильном треугольнике высоты являются и медианами и по свойству медианы точкой пересечения делятся в отношении 2:1, считая от вершины.
Точка пересечения - центр описанной окружности. СН=15, значит радиус
ОС=(2/3)*СН или R=(2/3)*15=10 (клеточек).
Ответ: R=10.
Второй вариант:
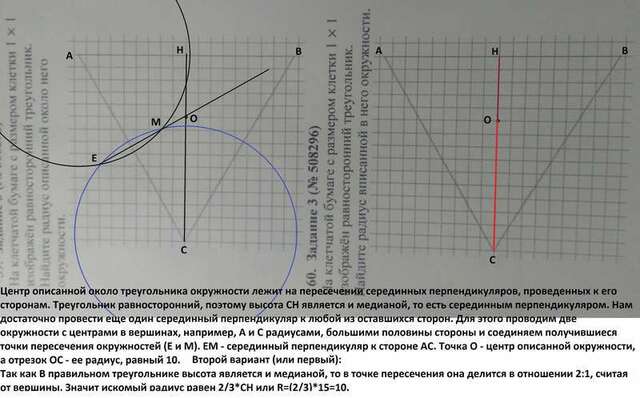
Центр описанной около треугольника окружности лежит на пересечении серединных перпендикуляров, проведенных к его сторонам. Треугольник равносторонний, поэтому высота СН является и медианой, то есть серединным перпендикуляром. Нам достаточно провести еще один серединный перпендикуляр к любой из оставшихся сторон. Для этого проводим две окружности с центрами в вершинах, например, А и С радиусами, большими половины стороны и соединяем получившиеся точки пересечения окружностей (Е и М). ЕМ - серединный перпендикуляр к стороне АС. Точка О - центр описанной окружности, а отрезок ОС - ее радиус, равный 10.