Вычислить площадь фигуры ограниченной линиями у=(х+2)^2,х=0 , у=0

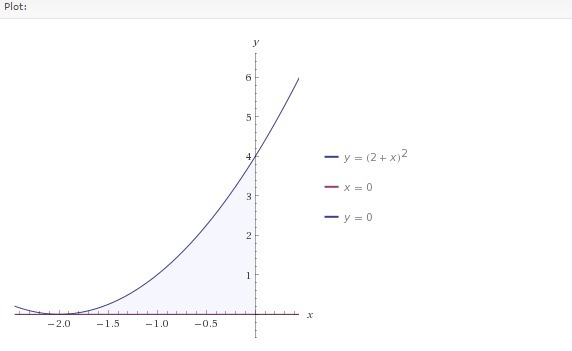
Для того чтобы вычислить площадь, ограниченную линиями, нужно построить эти линии в одной координатной плоскости. (см рисунок)
Далее необходимо вычислить определенный интеграл. Пределы его будут от -2 до 0 (пределы изменения х). По Формуле Ньютона-Лейбница найти ответ.
$\int\limits^0_{-2} {(x+2)^{2} } \, dx = \int\limits^0_{-2}( { x^{2} +4x+4}) \, dx = -\frac{8}{3} =-2.7$ кв. единиц.