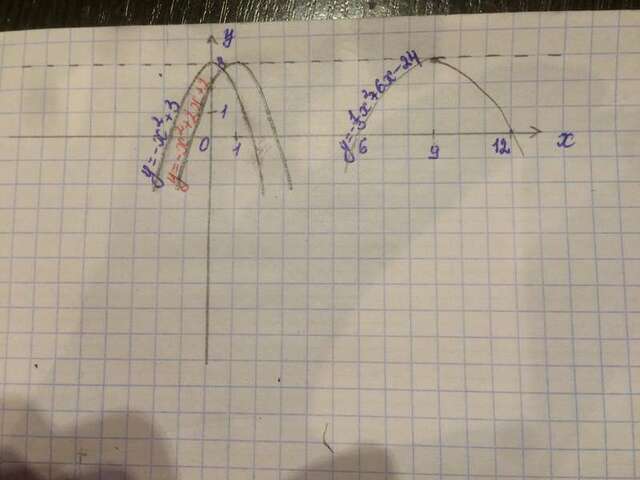
Так как графиком является парабола, то функция имеет вид  . Исходя из того, что значения функции не превосходят 3(то есть
. Исходя из того, что значения функции не превосходят 3(то есть  ), следует, что а<0(в этом случае ветви параболы направлены вниз).<br>Координаты вершины задаются формулами:
), следует, что а<0(в этом случае ветви параболы направлены вниз).<br>Координаты вершины задаются формулами:



 ;
; 
Осталось подобрать a, b, c.
Пусть а=-1, b=2, тогда 

Пусть а=-1, b=0, тогда 

Пусть а=-1/3, b=6, тогда