AB - диаметр окружности. Через точки A и B проведено две касательные к окружности. Третья...

Question

AB - диаметр окружности. Через точки A и B проведено две касательные к окружности. Третья касательная пересекает первые две в точках C и D. Доказать, что квадрат радиуса этой окружности равен произведению отрезков CA и DB. Заранее большое спасибо.

Answer 1

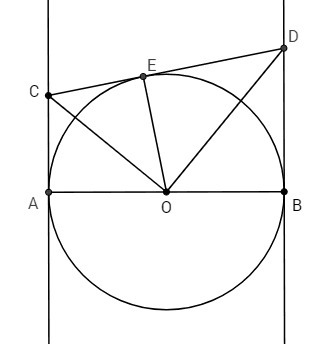
O - центр окружности
E - точка касания прямой CD и окружности

Отрезки касательных к окружности, проведенных из одной точки, равны.
CA=CE; DB=DE

△AOC=△COE; △EOD=△DOB (по трем сторонам)
∠AOC=∠COE; ∠EOD=∠DOB

∠AOC+∠COE+∠EOD+∠DOB =180° <=> 2∠COE +2∠EOD =180° <=> ∠COE+∠EOD =90° <=> ∠COD =90°

∠OEC =90° (касательная перпендикулярна радиусу, проведенному в точку касания)
OE - высота в прямоугольном треугольнике COD

Квадрат высоты, проведенной из вершины прямого угла, равен произведению проекций катетов на гипотенузу.
OE^2= CE*DE <=> OE^2= CA*DB

---

Comments

Благодарю