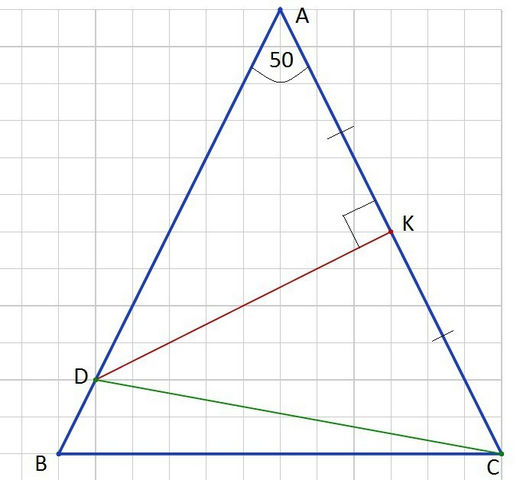
Так как треугольник АВС равнобедренный, то уголы АВС и АСВ равны. Найдём их:
Сумма углов треугольника равна 180°, значит можно записать:
∠АВС+∠АСВ=180°-50°=130°
А так как углы равны, то ∠АВС=∠АСВ=130°:2=65°
Далее рассмотрим треугольник ADC. В нём DK - серединный перпендикуляр, следовательно АК=КС. Значит треугольник ADC равнобедренный и ∠DAC=∠DCA=50°.
Угол АСВ состоит из углов DCA и DCB, можно записать
∠АСВ=∠DCA+∠DCB ⇒ ∠DCB=∠ACB-∠DCA
Подставляем найденные ранее значения углов и находим ∠DCB:
∠DCB=65°-50°=15°
Ответ: ∠DCB=15°