В правильной треугольной пирамиде сторона основания составляет 0.5 высоты пирамиды....

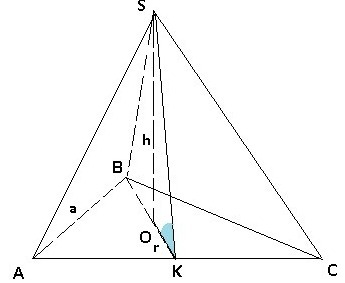
Задание. В правильной треугольной пирамиде сторона основания составляет 0.5 высоты пирамиды. Найдите апофему пирамиды, если её объем равен 36 корней из 3 см³.
Решение:
По условию сторона основания составляет 0,5 высоты пирамиды, т.е. a = 0,5h. Тогда площадь основания равна: $S_o= \dfrac{ \sqrt{3} a^2}{4} = \dfrac{h^2 \cdot\sqrt{3} }{16}$
Объем пирамиды вычисляется по формуле $V= \frac{1}{3} \cdot S_o\cdot h$ .
$36 \sqrt{3} = \dfrac{1}{3} \cdot\dfrac{h^2 \cdot\sqrt{3} }{16} \cdot h\\\\ h^3=36\cdot48\\ \\ h= 12\,\,_{CM}$
Тогда сторона основания равна $a=0.5h=0.5\cdot12=6\,\, _{CM}$ . Радиус вписанной окружности основания : $OK=r =\dfrac{a}{2 \sqrt{3} } = \dfrac{6}{2 \sqrt{3} } = \sqrt{3}$ см.
Найдем апофему SK по т. Пифагора для прямоугольного треугольника SOK, т.е. $SK= \sqrt{SO^2+OK^2} = \sqrt{12^2+(\sqrt{3})^2} = \sqrt{147}$ см

Ответ: $\sqrt{147}$ cм.