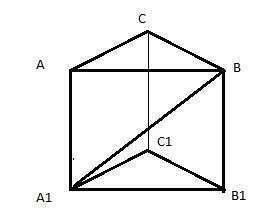
Построим правильную треугольную призму АВСА1В1С1 и проведем
диагональ боковой грани А1В.
Правильная треугольная призма — призма, в основаниях
которой лежат два правильных треугольника, а все боковые грани строго
перпендикулярны этим основаниям.
Формула площади боковой поверхности
призмы S=p*h, где р - периметр основания, h – высота
р=3*3=9 см (так как призма правильная)
Найдем высоту данной призмы АА1:
Рассмотрим треугольник АВА1:
Угол ВАА1 – прямой (так как
призма правильная),
АВ=3 см – катет данного
треугольника
ВА1=5 см – гипотенуза данного
треугольника
По теореме Пифагора найдем
второй катет:
АА1=√(ВА1^2 – AB^2)=√(5^2-3^2)=√(25-9)=√16=4 см
Боковая площадь данной призмы равна
S=p*h=9*4=36 кв. см.