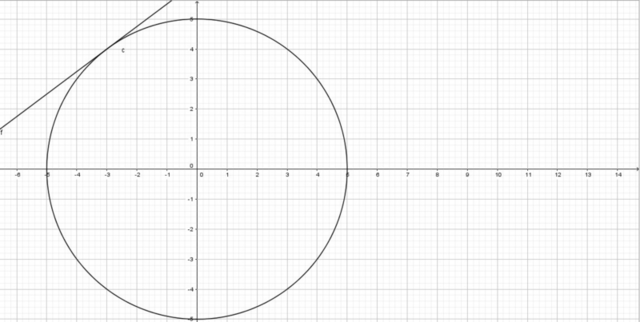
Задание. Докажите, что прямая 3x−4y+25=0 касается окружности x^2+y^2=25. Найдите сумму координат точки касания.
Решение:
 - уравнение окружности с центром (0;0) и радиусом R=5. А 3х-4у+25=0 - уравнение прямой, проходящая через точки (-3;4), (0;6.25). Точка касания - (-3;4). Сумма координат точки касания равна -3+4 = 1
- уравнение окружности с центром (0;0) и радиусом R=5. А 3х-4у+25=0 - уравнение прямой, проходящая через точки (-3;4), (0;6.25). Точка касания - (-3;4). Сумма координат точки касания равна -3+4 = 1
Ответ: 1.