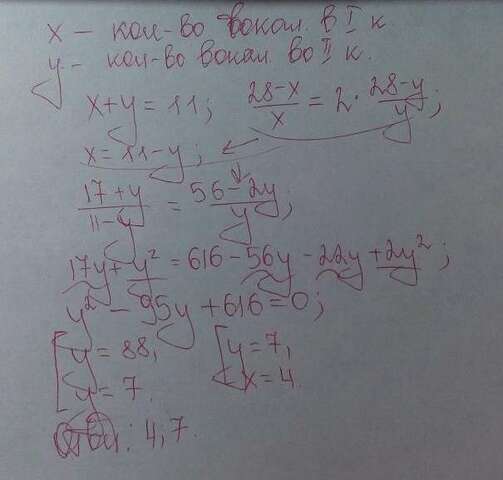В двух коллективах песни и пляски по 28 человек в каждом, было 11 вокалистов, остальные...

Question

В двух коллективах песни и пляски по 28 человек в каждом, было 11 вокалистов, остальные танцоры. Сколько вокалистов было в каждом коллективе, если известно, что в первом отношение числа танцоров к числу вокалистов было в 2 раза больше, чем это же отношение во втором коллективе?

Answer 1

Довольно милая задачка, сводящаяся к решению квадратного уравнения. Само решения я вложила в качестве фото, а сейчас объясню его суть.
Пусть x - количество вокалистов в первом коллективе, y - во втором. Тогда очевидно, что (28-x) и (28-y) - это количества танцоров в первом и втором коллективах соответственно. Из условия:
x+y=11; (28-x)/x=2*(28-y)/y. 
Это БАНАЛЬНАЯ система двух уравнений. Из первого условия выражаем, например, x и подставляем во второе. Далее сводим дробно-рациональное уравнение к квадратному (исходя из условия, что ни количество танцоров, ни количество вокалистов не может быть равно нулю).
Квадратное уравнение я решала с помощью теоремы Виета, но можно считать дискриминант, хотя это долгий и неблагодарный труд. Получаем корни: 7 и 88. Количество вокалистов не может быть больше числа участников коллектива, поэтому x=88 не подходит по условию. Следовательно, y=7, а x=11-7=4.

---