Точка i центр окружности s1 вписанной в треугольник abc точка o центр окружности s2...

Question

Точка i центр окружности s1 вписанной в треугольник abc точка o центр окружности s2 описанной около треугольника bic. а) докажите что точка o лежит на окружности описанной около треугольника abc.

Answer 1

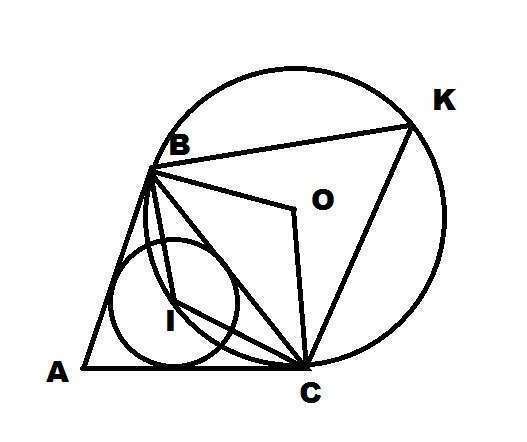
Пусть угол BAC = α

∠ABC + ∠ACB = 180° - α

∠IBC + ∠ICB = (180° - α)/2 = 90° - α/2 (т.к. центр вписанной окружности лежит в точке пересечения биссектрис)

∠BIC = 180° - (∠IBC + ∠ICB) = 180° - 90° + α/2 = 90° + α/2

∠BKC = 180° - ∠BIC = 180° - 90° - α/2 = 90° - α/2 (сумма противоположных углов четырехугольника вписанного в окружность равна 180°)

∠BOC - центральный углу ∠BKC => ∠BOC = 2*∠BKC = 2*(90° - α/2) = 180° - α

т.к. ∠BAC + ∠BOC = α + 180° - α = 180°, то около ABOC можно описать окружность, но это та же окружность, которая описана около треугольника АВС и на ней лежит точка О. Что и требовалось доказать

Ответ: доказано.

---

Comments

а что это за точка К?

---

любая точка на большой окружности

---

Честно говоря не любитель задач с дополнительным построение и если возможно, то стараюсь от него воздерживаться, чтоб не путать людей.

---

На мой взгляд было бы удобнее сначала найти большую дугу BC = 180+α, а затем найти меньшую дугу BC = 180-α и из этого уже следует, что ∠BOC будет равен 180-α. Так нам не придется строить точку K которая смущает людей )