ДУМАЕМ
Надо найти точки где первая производная функции равна 0.
1)
ДАНО
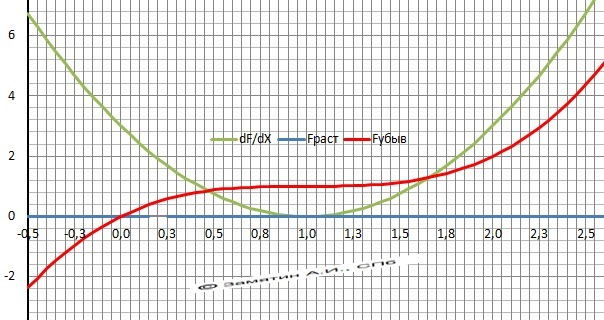
F(x) = x³ - 3x²+3x
РЕШЕ:НИЕ
F'(x) = 3x² - 6x + 3 = 0 - точки экстремумов.
Сократили на 3 и получили квадратное уравнение
y = x² - 2x+1 = 0
Решаем и получаем корни - х1 =х2 = 1 - по оси Х.
Находим координату У.
У(1) = -1-3 +3 = - 1
Точка касательной - А(1,1) - график в приложении.
2)
ДАНО
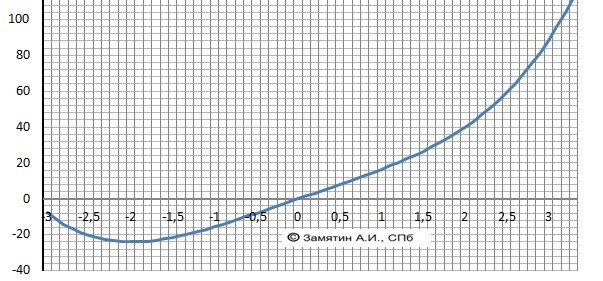
F(x) = 1/2*x⁴ + 16*x
РЕШЕНИЕ
Находим корни производной
F'(x) = 2x³ + 16 = 0
x³ = 16: 2 = - 8
x = ∛8 = -2 - по оси Х.
Находим координату У - подстановкой - х=2.
у = 8/2 + 16*2 = 8 - 32 = -24
ОТВЕТ А(-2,-24)
График функции в приложении.