Основания равнобокой трапеции равны 12 см и 18 см, а диагональ является биссектрисой её...

Question

Дано ответов: 2

Artyom121199_zn · Answer 1 · 2018-05-16T05:53:16+0000

Биссектриса угла в трапеции отсекает от противолежащего основания отрезок, равный боковой стороне (свойство трапеции).Так как биссектрисой является диагональ, то ВС=СД.
На основание АД опустим высоту СМ. МД=АД-АМ=АД-ВС=18-12=6 см.
В тр-ке СМД СМ²=СД²-МД²=12²-6²=108,
СМ=6√3 см.
Площадь трапеции: S=(АД+ВС)·СМ/2=(12+18)·6√3/2=90√3 см² - это ответ.

Юленька194_zn · Answer 2 · 2018-05-16T05:53:17+0000

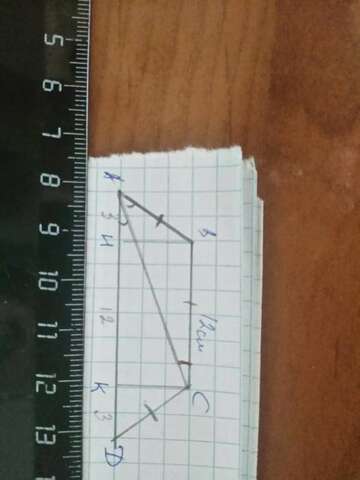
Дано: АВСД - трапеция, ВС=12 см, АД=18 см, АС- биссектриса угла А
Найти S трапеции

Решение:
1) ВС||АД, АС - секущая. Значит ∠ВСА=∠САД как накрест лежащие.
2) ∠ВАС=∠САВ , потому что АС- биссектриса.
∠ВСА=∠САД как накрест лежащие. (см. пункт 1)
Отсюда следует, что ∠ВАС=∠ВСА.
3) Рассмотрим треугольнике АВС. Он равнобедренный, так ка углы при основании равны.(∠А=∠С из пункта 2). Значит АВ=ВС=12 см
4) Рассмотрим ΔАВН. ВН- высота, АВ=12 см, АН= $\frac{AD-BC}{2} = \frac{18-12}{2} = \frac{6}{2} =3$ см. Этот треугольник прямоугольный, поэтому по теореме Пифагора найдём катет ВН
ВН= $\sqrt{AB^2-AH^2}= \sqrt{12^2-3^2}= \sqrt{(12-3)(12+3)} = \sqrt{9*15}=3 \sqrt{15}$ см
5) Найдем площадь трапеции
$S= \frac{DC+AD}{2}*BH= \frac{12+18}{2}*3 \sqrt{15} =15*3 \sqrt{15} = 45 \sqrt{15}$ см²