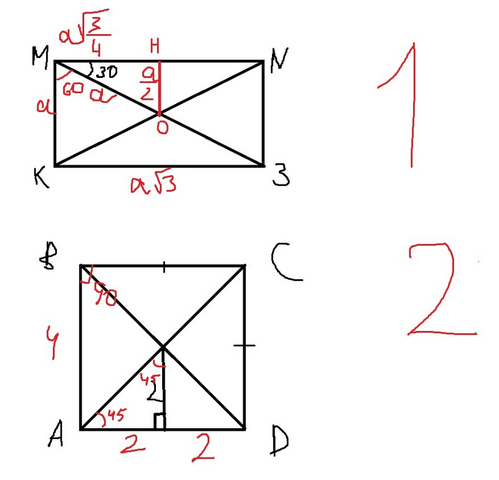
Давай начнем с верхней задачи.
Обозначим точку пересечения KN и MЗ как O.
Отрезок MO имеет длину a.
Тогда, проводим медиану OH к стороне MN, H - середина MN.
Получается прямоугольный треугольник MOH, в нем угол М = 30 градусов, а против угла 30 градусов лежит катет, равный половине гипотенузы (MO) - a/2, тогда MH по теореме пифагора = корень(a квадрат - а квадрат /4) = корень(3а квадрат /4 )=a*корень из 3/4, следовательно сторона HN равна такому же числу, а сторона MN = 2 * MH, тогда MN=а на корень из 3, сторона КЗ тоже равна MN.
Угол KMN = 90 градусов, а угол NMO= 30 градусов, тогда угол KMO = 90-30=60 градусов., угол MKO аналогично, значит, треугольник MKO равносторонний, и его сторона MK = a
Находим периметр: a+a+a*корень из 3+а*корень из 3=2а+2а корень из 3= 2а(1+корень из 3)
Вторая задача попроще:
Пересечение диагоналей точка - О.
OK=AK, т.к. OAK и KOA= 45 градусов. а значит AD=2AK=4
и периметр 4*4=16