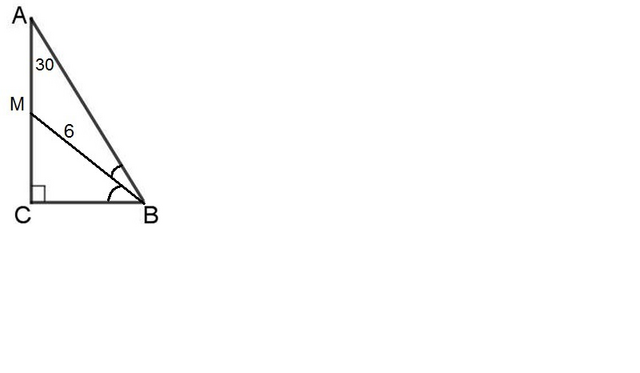Задача 1.висоти BD і CE трикутника ABC перетинаються в точці М .Здайдіть кут ABC, якщо...

Question

Задача 1.
висоти BD і CE трикутника ABC перетинаються в точці М .Здайдіть кут ABC, якщо кут ACB=45°, кут BMC=70°
Задача 2.
У трикутнику ABC кут С=90°, кут А=30°, відрізок BM -бісектриса трикутника. Знайдіть довжину катета AC ,якщо ВМ=6 см.

Помогите пожалуйста решить геометрія

Answer 1

Задача 1.
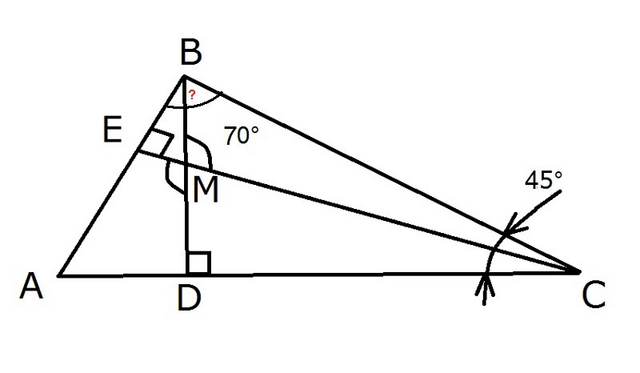
∠BMC = ∠EMD = 70° (вертикальные углы).
Рассмотрим четырехугольник AEMD:
∠BAC = 360° - (∠AEM + ∠ADM +∠EMD) (сумма углов четырехугольника = 360°)
т.к. BD и CE - высоты (по усл) , то ∠AEM = ∠MDA = 90°.
Найдем ∠BAC:
∠BAC = 360° - (90° + 90° + 70°) = 110°
∠ABC = 180° - (∠ACB + ∠BAC) (сумма углов треугольника = 180°)
∠ABC = 180° - (45° + 110°) = 25°.
Ответ: 25°

Задача 2.
Т.к. BM - биссектриса, то ∠CBM=∠MBA
Рассмотрим ΔABC: ∠C=90° (по усл), ∠A=30° (по усл) ⇒ 
∠B = 180° - (90°+30°)=60°⇒ ∠CBM=∠MBA=1/2∠B=30°
Рассмотрим ΔAMB: ∠MAB = ∠ABM ⇒ треугольник равнобедренный ⇒ MA=MB=6 см
Рассмотрим ΔCMB: ∠C=90°, ∠MBC=30°. Вспоминаем, что катет, лежащий против угла 30° равен половине гипотенузы ⇒MC = 1/2 MB = 3 см
AC = AM + MC = 6 см + 3 см = 9 см

---

---