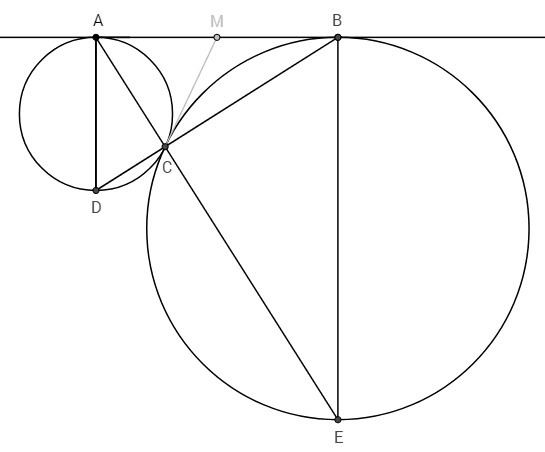
AD, BE - диаметры окружностей. AD, BE перпендикулярны касательной AB. DAB и ABE - прямоугольные треугольники.
Общая касательная, проходящая через точку С, пересекает AB в точке M. Отрезки касательных к окружности, проведенных из одной точки, равны. MA=MC=MB. Если медиана треугольника равна половине стороны, к которой она проведена, то угол напротив этой стороны равен 90. ∠ACB=90. Плоский угол, опирающийся на диаметр окружности, - прямой. ∠ACD=90. ∠DCB - развернутый угол; точка С лежит на отрезке DB. Аналогично, точка С лежит на отрезке AE.
∠ADB= 90-∠ABD =90-∠ABC
∠BAE= ∠BAC =90-∠ABC
∠ADB=∠BAE
Треугольники DAB и ABE подобны по двум углам.
AD/AB=AB/BE <=> AB^2=AD*BE <=> AB^2=2*16 <=> AB=4√2 (~5,65)
Углы в основаниях треугольников ACD и BCE равны как накрест лежащие при параллельных AD и BE. Треугольники ACD и BCE подобны.
AD/AC=BE/CE <=> AC/CE=AD/BE <=> AC/CE=1/8 <=> CE=8AC
В прямоугольном треугольнике квадрат высоты, проведенной из вершины прямого угла, равен произведению проекций катетов.
BC^2=AC*CE <=> BC^2=8AC^2
AB^2=AC^2 +BC^2 <=> AB^2= 9AC^2 <=> AC=AB/3 <=> AC=4√2/3 (~1,89)
BC=√(AB^2 -AC^2) <=> BC=√(32 -32/9)= 16/3 (~5,33)