Точки соприкосновения вписаного круга делит гипотенузу прямоугольного треугольника на...

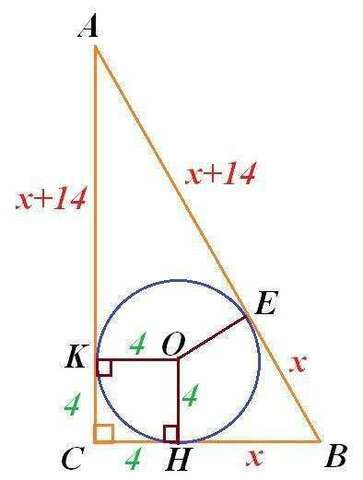
Рассмотрим прямоугольный ΔАВС и вписанный в него круг с центром О и радиусом 4см.
Пусть К,Е и Н -точки касания круга сторон треугольника.
По свойству отрезков касательных, проведенных к окружности из одной точки, получим: АЕ=АК, ВЕ=ВН, СК=СН.
Т.к. ОН=ОК=4см - радиусы, проведенные в токи касания, то ОН⊥CН и ОК⊥СК. Значит, СКОН - квадрат со стороной 4см.
СК=СН=4см.
Пусть ВЕ=х см, тогда АЕ=х+14 см.
Следовательно, АК=х+14 см, ВН=х см, АВ=14+2х см, АС=х+18 см, СВ=х+4 см.
С одной стороны площадь ΔАВС:
$S_{\Delta ABC}= \frac{1}{2} P_{\Delta ABC}*r= \frac{AB+BC+AC}{2} *OH=\\=\frac{(2x+18)+(x+18)+(x+4)}{2} *4=2(4x+36)=8(x+9)$
С другой стороны эту же площадь можно найти так:
$S_{\Delta ABC}= \frac{1}{2} AC*BC= \frac{1}{2} *(x+18)(x+4)$
Решаем уравнение:
0,5(х+18)(x+4)=8(x+9)
x²+22x+72=16x+144
x²+6x-72=0
x=6 или х=-12
По смыслу задачи х=-12 не удовлетворяет требованию положительности длины отрезка.
Значит, х=ВЕ=6см.
Тогда, $S_{\Delta ABC}=8(x+9)=8(6+9)=120$ (см²)
Ответ: 120 см².

Точки соприкосновения вписаного круга делит гипотенузу прямоугольного треугольника **...