Вычислить площадь фигуры ограниченной линиями y=x^2 и y=2x+3

ВСПОМИНАЕМ
Площадь фигуры - интеграл разности функций.
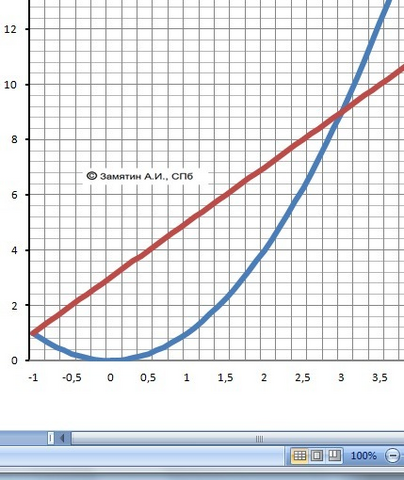
Графики функций в подарок.
РЕШЕНИЕ
1 - находим пределы интегрирования
х² = 2х + 3
Получаем квадратное уравнение
х² - 2х - 3 =0
Находим два корня
b = х1 = -1 и a = х2 = 3.
ВАЖНО!!! Прямая выше параболы - разность функции в расчете.
$S = \int\limits^3_b {(2x+ 3-x^2)} \, dx = - \frac{x^3}{3}+x^2+3x =9 - (-1 \frac{2}{3})=10 \frac{2}{3}$
ОТВЕТ 10 2/3 (10,667)