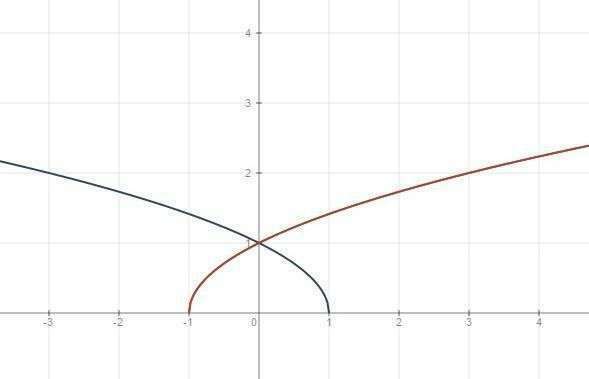
-y²+x+1≥0 y²≤x+1
y²-x+1≥0 y²≥x-1
cм. график -1 ≤х≤1 0≤ у≤1
========================
2. z=e^(2x-y²)
dz=z'ₓdx+z'ydy
dz=e^(2x-y²)*2dx+e^(2x-y²)*(-2y)dy
z=√x*arctgy² z'x=arctgy²/2√x z'y=√x*2y/(1+y⁴)
dz=arctgy²dx/2√x+2y√x*dy/(1+y⁴)
3. w=(u³-3v)² = u⁶-6u³v+9v² w'u=6u⁵-18vu² w'v=-6u³+18v
w''u,u=30u⁴-36vu w''v,v=18 w''u,v=w''v,u =-18u²
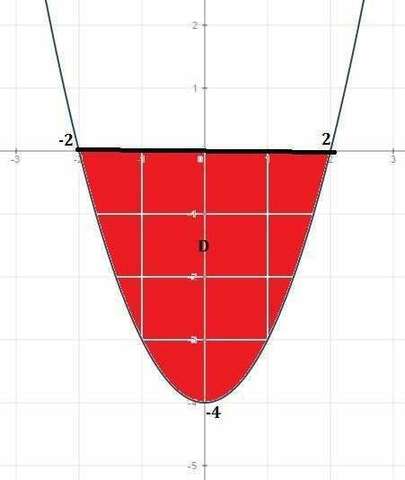
4. z=x²y-4y найти максимум в области y=x²-4 y=0 cм.график области приложен.
a) стационарные точки z'x=0 z'y=0 z'x=2xy=0 z'y=x²-4=0
x=0 y=0 z(0;0)=0
b) на границе области z=x²(x²-4)-4(x²-4) = x⁴-4x²-4x²+16=x⁴-8x²+16
z'=4x³-16x=4x(x-2)(x+2) x=0 y=-4 z(0;-4) = 16
x =2 y=0 z=0 x= -2 y=0 z=0
на прямой y=0 z=0
c) в угловых точках x=+-2 z=0
наибольшее значение 16 в точке (0;-4)