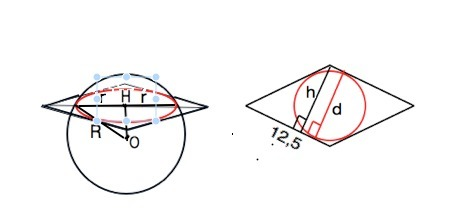
Плоскость пересекает шар по окружности. Для ромба эта окружность - вписанная, ее диаметр равен высоте ромба ( см. рисунок)
Отрезок, проведенный из центра шара к центру плоскости сечения перпендикулярен этой плоскости и является катетом прямоугольного треугольника, где второй катет - радиус окружности, а гипотенуза - радиус шара.
Обозначим центр шара О, центр окружности в сечении Н, радиус сечения r, радиус шара R.
По т.Пифагора r=√(R²-OH²)=√(100-64)=6 см
h=d=2r=12 см
Площадь ромба равна произведению его стороны и высоты.
S=a•h=12,5•12=150 см²