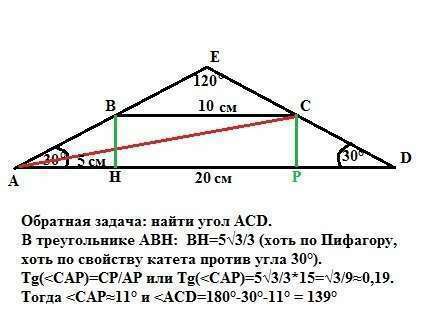
1. Сначала я докажу, что АС НЕ МОЖЕТ БЫТЬ биссектрисой угла BAD (то есть угла А) и Для этого продолжим боковые стороны АВ и DC до их пересечения в точке Е. Треугольник АЕD равнобедренный и в нем отрезок ВС является средней линией, так как он параллелен основанию AD и равен его половине. Следовательно, точки В и С делят боковые стороны треугольника пополам.
Углы при основании равны 30°, значит угол при вершине равен 120° (так как сумма углов треугольника равна 180°).
Отметим, что cos120°=cos(180-60)=-cos60° и по теореме косинусов найдем боковую сторону нашего треугольника. Пусть она равна Х,
тогда AD²=X²+X²-2*X*X*Cos120° или 400=2X²+2X²(1/2). Или
400=3*X² или 20=X√3.
Отсюда Х=20/√3=20√3/3 см. Это боковая сторона. Тогда половина этой стороны АЕ, то есть АВ=10√3/3 ≈5,8 см и треугольник АВС НЕ РАВНОБЕДРЕННЫЙ, а значит
АС - НЕ БИССЕКТРИСА угла ВАD и 2. Найдем периметр трапеции, не опираясь на не верное условие задачи. В равнобедренной трапеции высота, опущенная из тупого угла на основание, делит его на два отрезка, меньший из которых равен полуразности двух оснований. Пусть ВН - высота, тогда
АН=(20-10)/2=5см. В прямоугольном треугольнике АВН катет ВН лежит против угла 30° (дано). Значит АВ²=АВ²/4 + АН² или 3АВ²=100.
Отсюда АВ=10/√3=10√3/3. Мы видим, что этот ответ совпадает с полученным результатом в п1.
Таким образом, периметр трапеции равен
Р=20+10+2*(10√3/3)=30+20√3/3 см.
Р=30+20√3/3.
Теперь посмотрим, что же хотел получить в ответе составитель этой задачи.
Если <АСВ=180°-135°-30°=15°, то есть <br>Тогда АВС - равнобедренный треугольник и АВ=ВС.
Периметр равен 10+10+10+20=50см.