Я только про внешние - мне интересен подход к задаче, я ради него и выкладываю решение.
На сторонах произвольного треугольника построены правильные треугольники. Доказать, что центры тяжести этих треугольников - вершины правильного треугольника.
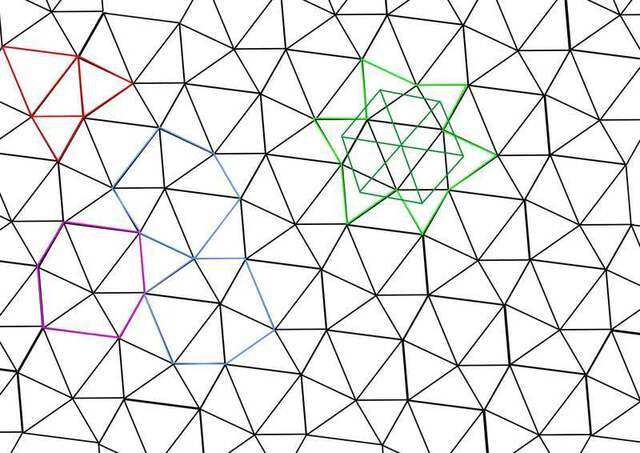
Прежде, чем начать доказательство, взгляните на чертеж.
На чертеже представлено периодическое покрытие плоскости треугольниками, соответствующее условию задачи. Собственно условие обведено красным в левом верхнем углу чертежа (просто для демонстрации). На плоскости присутствуют треугольники, полученные простым смещением исходного, а также - полученные их них поворотом на 120 и 240 градусов (и правильные треугольники треух разных в общем случае размеров). Само покрытие (на практике) получено просто параллельным переносом фигуры, обведенной фиолетовым цветом. Это неправильный шестиугольник с параллельными противоположными сторонами. Тут могут возникать вопросы типа "а почему стороны параллельны?". Это очень просто доказывается сравнением углов между прямыми (по сути там везде задействованы углы исходного треугольника и угол 60 градусов).
В качестве ячейки можно было бы выбрать любой из вариантов, обведенных сиреневым цветом, эти ячейки получаются из фиолетового поворотами на 120 и 240 градусов.)
Теперь - доказательство.
В правой стороне чертежа изображена неправильная шестивершинная звезда. Построена она так - выбран какой-то правильный треугольник (проще всего, если - с максимальной стороной). К каждой из его сторон "пристроены" треугольники, равные исходному, а на их сторонах построены правильные треугольники (напоминаю, все это является частью покрытия, то есть возникло просто в результате многократного размножения фиолетовой ячейки). Легко видеть, что если соединить центры треугольников при вершинах звезды (темно зеленый шестиугольник), то эта фигура будет инвариантна относительно поворотов на 120 и 240 градусов (вокруг центра "большого правильного треугольника в центре звезды) - то есть у них равны стороны "через одну". Но также очевидно, что равны противоположные стороны, они получаются друг из друга параллельным сдвигом. Вместе эти два утверждения означают, что это правильный шестиугольник (можно увидеть равенство сторон и по другому - они соединяют сходственные точки в разных "ячейках"). Диагонали этого шестиугольника проходят через центр симметрии фигуры и делят его на 6 правильных треугольников, каждый из которых завершает доказательство - вершины каждого из них удовлетворяют задаче.
И ни одной формулы. :)