(Рисунок схематичный на готовой призме)
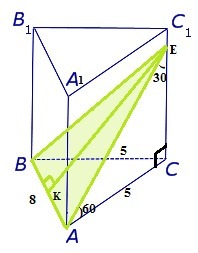
Пусть ABCA₁B₁C₁ - прямая призма, в основании которой лежит равнобедеренный треугольник ABC. Через основание (AB) треугольника ABC проведено сечение так, что ∠C₁AC = ∠С₁BC = 60°. Сечение пересекает ребро C₁C в точке E.
Треугольник ACE = треугольнику BCE по двум сторонам и углу между ними:
AC = BC как боковые стороны равнобедренного треугольника ABC
СЕ - общая сторона
∠ACE = ∠BCE = 90°, т.к. призма прямая
⇒ AE = BE ⇒ сечение ABE- равнобедренный треугольник с основанием AB, боковыми сторонами AE u BE
В прямоугольном треугольнике ACE:
∠ACE = 90°
∠EAC = 60°
∠AEC = 180 - 90 - 60 = 30 (°)
Катет AC = 5 cм лежит против ∠AEC = 30°. Такой катет равен половине гипотенузы.
Гипотенуза AE = AC * 2
AE = 5 * 2 = 10 (см)
Площадь равнобедренного треугольника равна произведению высоты, проведенной к основанию на половину длины основания.
EK - высота (также медиана и биссектриса), проведенная к основанию треугольника ABE. ⇒ AK = AB / 2
AK = 8 / 2 = 4 (cм)
По теореме Пифагора:
AE² = AK² + EK²
EK² = AE² - AK²
EK² = 10² - 4² = 100 - 16 = 84
EK = √84 = 2√21 (см)
S(ABE) = EK * AK
S(ABE) = 2√21 * 4 = 8√21 (см²)