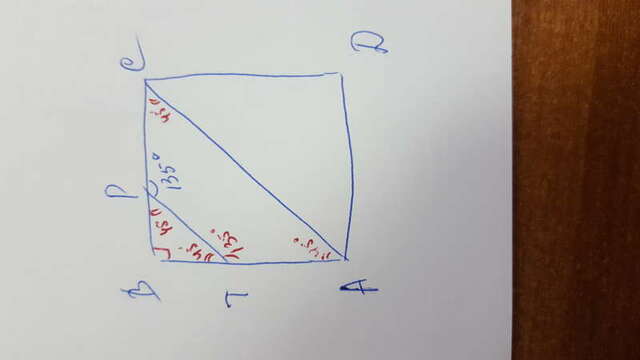
Четырехугольник можно вписать в окружность, если у него суммы противоположных углов равны 180°
т.е. ATPC должно выполнятся равенство: ∠CAT+∠TPC=∠ATP+∠PCA=180°
проверим.
∠TPC=135° - по условию
∠CAT=∠PCA=45° (по свойству диагонали квадрата, АС-диагональ квадрата)
осталось найти ∠ATP
либо можно найти угол так:
∠TPC+∠TPB=180° - смежные⇒∠TPB=45°
ΔTPB - прямоугольный (∠TВP=90°, т.к. ABCD - квадрат)
тогда ∠PTB=90°-45°=45°
∠PTB+∠ATP=180° -смежные⇒∠ATP=180° -45°=135°
либо ∠ATP можно найти угол так:
∠TPC+∠PCA=135°+45°=180° - внутренние односторонние при прямых TP и AC, и секущей PC ⇒ TP║AC ⇒∠ATP+∠СAT=180° (внутренние односторонние)
∠СAT=45° - по свойству диагонали квадрата, АС-диагональ квадрата
∠ATP=180°-45°=135°
Все углы нашли, теперь проверяем, выполняется ли условие
∠CAT+∠TPC=∠ATP+∠PCA
45°+135°=135°+45°
180°=180°
Ответ: вокруг четырехугольника ATPC можно описать окружность
(чертеж во вложении)