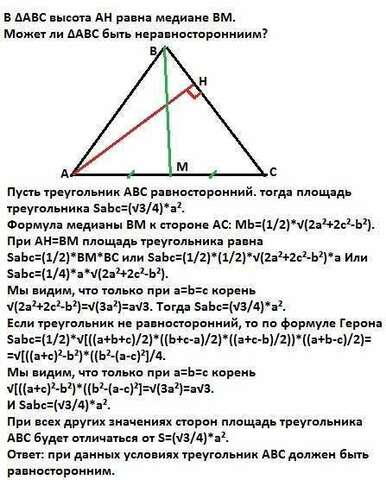
Пусть треугольник АВС равносторонний. Тогда площадь треугольникаSabc=(√3/4)*а².Формула медианы ВМ к стороне АС: Mb=(1/2)*√(2a²+2c²-b²).При АН=ВМ площадь треугольника равнаSabc=(1/2)*BM*BC или Sabc=(1/2)*(1/2)*√(2a²+2c²-b²)*а. ИлиSabc=(1/4)*а*√(2a²+2c²-b²).Мы видим, что только при a=b=c корень √(2a²+2c²-b²)=√(3a²)=а√3.Тогда Sabc=(√3/4)*а².Если треугольник не равносторонний, то по формуле Герона Sabc=(1/2)*√[((a+b+c)/2)*((b+c-a)/2)*((a+c-b)/2))*((a+b-c)/2)=
=√[((a+c)²-b²)*((b²-(a-c)²]/4.Мы видим, что только при a=b=c корень
√[((a+c)²-b²)*((b²-(a-c)²]=√(3a²)=а√3. И Sabc=(√3/4)*а².При всех других значениях сторон площадь треугольника АВС будет отличаться отS=(√3/4)*а².Ответ: при данных условиях треугольник АВС должен быть равносторонним.