Параллельные прямые AC и BD пересекают плоскость α в точках A и B. Точки C и D лежат по...

Question

Параллельные прямые AC и BD пересекают плоскость α в точках A и B. Точки C и D лежат по одну сторону от плоскости α. AC=14 см, BD=12 см, AB=13 см.
Докажите, что прямая CD пересекает плоскость α в некоторой точке E. Вычислите длину отрезка AE.

Answer 1

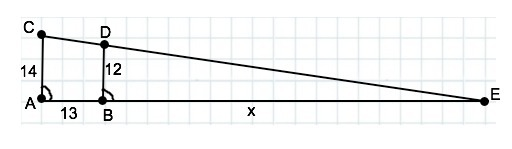
Отрезки параллельных прямых, заключенные между плоскостью и параллельной ей прямой, равны. 

АС параллельна ВD, но  не равна ей,  следовательно, СЕ не параллельна плоскости α и пересекает ее в некоторой т.Е.

АС║BD ⇒ лежат в одной плоскости;  т. Е принадлежит прямой CD и лежит в той же плоскости. 

 В ∆ АСЕ точка B принадлежит АЕ, точка D принадлежит СЕ,  BD|║АС по условию, ⇒ треугольники АСЕ и BDE подобны. 

Из подобия следует отношение:

  АС:BD=АЕ:ВЕ.

Примем длину ВЕ=х

14:12=(13+х):х. 

14 х=156+12 х⇒

х=78

АЕ=13+78=91 см

---