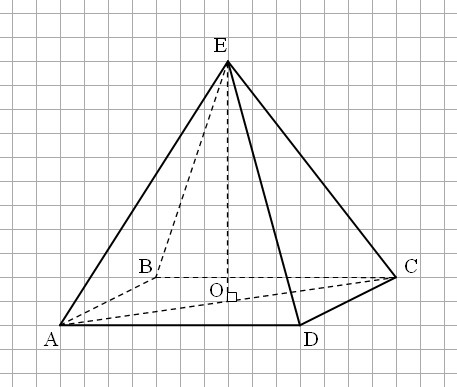
Так как диагональное сечение правильной четырехугольной пирамиды представляет из себя два равных прямоугольных треугольника с катетами: АО, равным половине диагонали основания, и ОЕ, равным высоте пирамиды, то:
Sсеч. = 1/2 АС*ОЕ
Сторона основания пирамиды: а = √S = √36 = 6 (см)
Диагональ основания пирамиды: АС = √2а² = 6√2 (см)
Тогда:
Sсеч. = 3√2 * 5 = 15√2 (см²)
Ответ: 15√2 см²