Исследовать функцию и построить график : y=2x^4-x^2+1

Question

Дан 1 ответ

Правильный ответ

Ищем область определения:
D(y)∈R
ищем 1 и 2 производные:
$y'=2*4x^3-2x=8x^3-2x$
$y''=8*3x^2-2=24x^2-2$
определяем критические точки:
$8x^3-2x=0 \\4x^3-x=0 \\x(4x^2-1)=0 \\x_{1}=0 \\4x^2-1=0 \\4x^2=1 \\x^2= \frac{1}{4} \\x_2=\frac{1}{2}=0,5 \\x_3=-\frac{1}{2} =-0,5$
x=0; y=1; (0;1)
x=0,5; y=0,875 (0,5;0,875)
x=-0,5; y=0,875 (-0,5;0,875)
определяем максимум/минимум и возрастание/убывание:
определяем знак производной на каждом интервале:
1) на (-oo;-0,5]
берем например (-1):
$(-1)*(4*(-1)^2-1)=(-1)*3=(-3)$ - знак минус
2) на [-0,5;0]
берем например (-0,1):
$(-0,1)*(4*(-0,1)^2-1)=(-0,1)(-0,96)=0,096$ - знак плюс
3) на [0;0,5]
берем например 0,1:
$0,1*(4*(0,1)^2-1)=0,1*(-0,96)=-0,096$ - знак минус
4) на [0,5;+oo)
берем например 1:
$1*(4*1^2-1)=3$ - знак плюс
производная в точке (-0,5;0,875) меняет знак с минуса на плюс, значит это минимум.
производная в точке (0;1) меняет знак с плюса на минус, значит это максимум
аналогично для точки (0,5;0,875) - это 2 минимум
функция убывает на (-oo;-0,5] и [0;0,5]
и возрастает на [-0,5;0] и [0,5;+oo)
так как область определения этой функции - любое действительное число, то данная функция не имеет асимтот
проверяем четность:
$y(-x)=2(-x)^4-(-x)^2+1=2x^4-x^2+1=y(x)$ - значит функция четная
ищем интервалы выпуклости/вогнутости:
приравниваем 2 производную к 0:
$24x^2-2=0 \\12x^2-1=0 \\x^2= \frac{1}{12} \\x_1=\frac{1}{ \sqrt{12}}=\frac{1}{2 \sqrt{3}}=\frac{\sqrt{3}}{6 } \\x_2=-\frac{\sqrt{3}}{6 }$
определяем знаки:
$\frac{\sqrt{3}}{6 }$ ≈0,289
$-\frac{\sqrt{3}}{6 }$ ≈-0,289
1) на (-oo;-0,289]
берем например (-1):
$12(-1)^2-1=11$ - знак плюс
2) на [-0,289;0,289]:
берем например 0:
12*0-1=-1 - знак минус
3)
на [0,289;+oo)
берем например 1:
12-1=11 - знак +
значит функция выпукла на $[-\frac{\sqrt{3}}{6 };\frac{\sqrt{3}}{6 }]$
и вогнута на (-oo; $-\frac{\sqrt{3}}{6 }]$ и $[\frac{\sqrt{3}}{6 };$ ;+oo)
определяем пересечения с осями координат:
$y=0; \\2x^4-x^2+1=0 \\u=x^2 \\2u^2-u+1=0 \\D=(-1)^2-4*2*1=-7 \\D\ \textless \ 0$
x- нет корней, значит данная функция не пересекается с осью ox
x=0; y=1; (0;1)
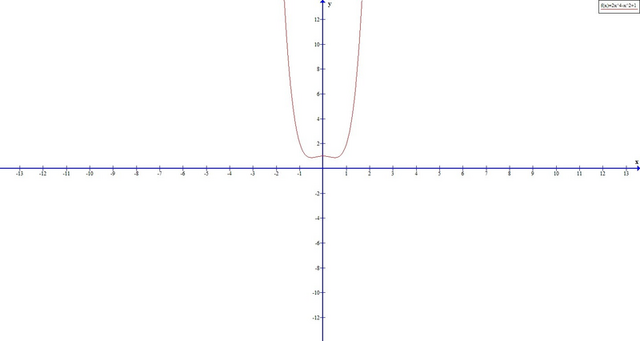
Подведем итоги:
функция: $y=2x^4-x^2+1$
область определения: D(y)∈R
функция непрерывна
1 производная: $y'=8x^3-2x$
2 производная: $y''=24x^2-2$
функция четная
функция не имеет асимптот
нули: (0;1)
экстремиумы: (0,5;0,875), (-0,5;0,875), (0;1)
максимум: (0;1)
минимум: (-0,5;0,875), (0,5;0,875)
убывает: (-oo;-0,5] и [0;0,5]
возрастает: [-0,5;0] и [0,5;+oo)
выпукла: $[-\frac{\sqrt{3}}{6 };\frac{\sqrt{3}}{6 }]$
вогнута: (-oo; $-\frac{\sqrt{3}}{6 }]$ и $[\frac{\sqrt{3}}{6 };$ ;+oo)
и строим график:

AnonimusPro_zn (149k баллов) 16 Май, 18