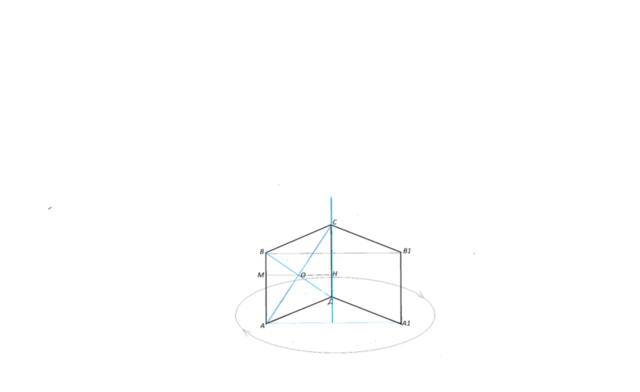
Площадь получившейся фигуры АВСВ1А1Д складывается из площадей боковой поверхности двух конусов -
верхнего ВСВ1 и
нижнего АДА1,- и
площади
боковой поверхности цилиндра АВВ1А1.
Формула площади боковой поверхности конуса через радиус (R) и образующую (L):
Sбок. кон.=πRL
Радиус конуса здесь равен высоте ромба.
Так как диагонали АС и ВД ромба пересекаются под прямым углом и точкой пересечения делятся пополам,
высоту ромба можно найти из прямоугольного треугольника СОД - точнее, половину высоты ромба.
Треугольник СОД- "египетский", поэтому
СД=5 (проверьте по т. Пифагора)
Высота в прямоугольном треугольнике равна произведению катетов, деленному на гипотенузу ( из формулы площади прямоугольного треугольника)
ОН=ОС*ОД:СД=4*3:5=
2,4 см
Высота
МН ромба вдвое длиннее и
равна 4,8 см
Sбок. кон.=πRL
Sбок. кон=4,8*5π=
24π см²
2 Sбок. кон= 2*24π=48π ( площадь боковая конусов ВСВ1+АДА1)
Формула площади боковой поверхности цилиндра
:
Sбок. цил=2πRh, и высота h здесь
равна стороне ромба АВ =5 см
Sбок. цил=2π4,8*5=
48π см ²
Полная площадь фигуры, образованной вращением ромба вокруг его стороны, равна
Sполн.= 48π+48π=
96π см²