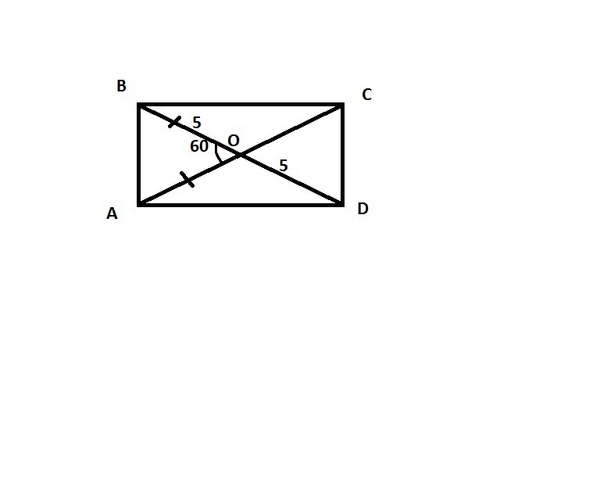
Пусть О - точка пересечения диагоналей прямоугольника. По свойству диагоналей прямоугольника d1 = d2. S прям = d² * sinα/2 = 10² * \frac{ \sqrt{3} }{2} / 2 = 25 \sqrt{3} . Рассмотрим треугольник AOB. угол АОВ = 60. По свойству градусных меру глов треугольника 180-60 = 120:2 = 60. Значит, треугольник АОВ равносторонний. АВ = 5 см. Sпрям = АB * BC. Зная площадь прямоуголька найдем вторую сторону.
25 \sqrt{3} = 5 * BC.
BC = 5 \sqrt{3} .
Меньшей стороной является AB = 5 см
Ответ: 5 см
P.s также сторону АВ можно вычислить с помощью теоремы косинусов.
АВ^{2} = АО^{2} +ОВ^{2} - 2*АО*АВ * cosα
АВ^{2} = 25 +25 - 50 * 1/2
АВ^{2} = 25
AB = 5