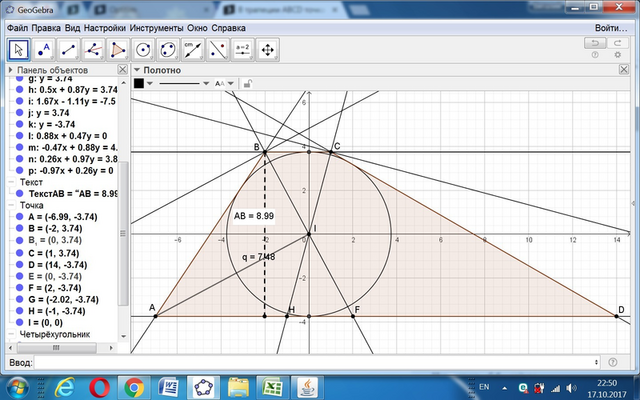
Если в трапеции ABCД точка I равноудалена о сторон трапеции, то точка I - центр вписанной окружности.
По свойству трапеции треугольники ABI и AIF прямоугольные и равные.
AF = 9. Значит, коэффициент деления стороны АД равен 9/3 = 3.
Деление стороны AД в отношении 3:4 (AF:FD), и 2:5 (AH:HD) заменим делением отрезков . АД = 3*7 = 21.
3:4 (AF:FD) = 9:12, 2:5 (AH:HD) = 6:15.
Сторона ВС равна отрезку FH = AF - AH = 9 - 6 = 3.
Сумма ВС + АД равна АВ + СД. СД = 3 + 21 - 9 = 15.
Обозначим проекцию АВ на АД за х.
Тогда высота трапеции как катеты треугольников с гипотенузами АВ и СД равна: 9² - х² = 15² - (18 - х)².
81 - х² = 225 - 324 + 36х - х².
36х = 180,
х = 180/36 = 5.
Тогда высота трапеции равна √(9² - 5²) = √(81 - 25) = √56 ≈ 7,483315.