Найдите площадь треугольника со сторонами, равным 5,6 и 7

Площадь треугольника можно вычислить разными способами. Ниже дается один из возможных вариантов - через нахождение высоты треугольника и затем по формуле S=a•h:2

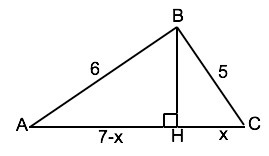
На рисунке в приложении стороны треугольника: АВ=6, ВС=5, АС=7,

ВH - высота, длину которой нужно найти.

По т.Пифагора

ВН²=АВ²-АН²

ВН²=ВС²-НС²

Приравняем значения ВН²

АВ²-АН²=ВС²-НС²

Примем НС=х и АН=7-х⇒

26-49+14х-х²=25-х²

Откуда $x= \frac{19}{7}$

По т.Пифагора из ∆ ВНС

$BH= \sqrt{5^2-( \frac{19}{7})^2 }= \frac{12 \sqrt{6} }{7}$

$S(ABC)= \frac{7*12 \sqrt{6} }{7*2} =6 \sqrt{6}$