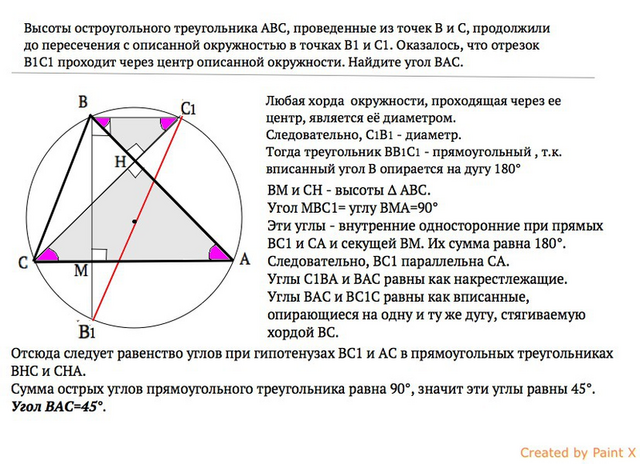
В окружности любая хорда, проходящая через её центр, является диаметром. Следовательно,
С1В1 - диаметр.
Тогда вписанный угол В1ВС1 прямой, т. к. опирается на дугу 180°.
Обозначим высоты ВМ и СН.
∠МВС1=∠ВМА=90°
Эти углы - внутренние односторонние при прямых ВС1 и СА и секущей ВМ, в сумме дают 180°. ⇒
ВС1║АС.
∠С1ВА=ВАС как накрестлежащие.
∠ВАС=∠ВС1С как вписанные, опирающиеся на одну и ту же дугу, стягиваемую хордой ВС.
Отсюда следует равенство углов при гипотенузах прямоугольных треугольников ВНС1 и СНА.
Сумма острых углов прямоугольного треугольника равна 90°, следовательно, в треугольнике АНС ∠А+∠С=90°, а т.к. они равны, то угол А=45°
Ответ:
∠ВАС=45°