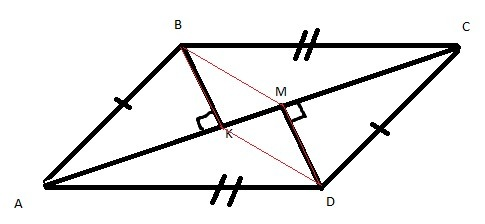
К одной и той же прямой проведено 2 перепендикуляра ВК и DM, значит, они параллельны друг другу.
По свойству параллелограмма, диагональ AC делит его на 2 равных прямоугольника ABC и ACD. Их площади (S) также равны. Получается:
S (ABC) = S (ACD)
AC*BK/2 = AC*DM/2 =>
ВК = DM
Т.к. ВК = DM и при этом BK || DM, можно заключить, что четырехугольник BMDK - параллелограмм.