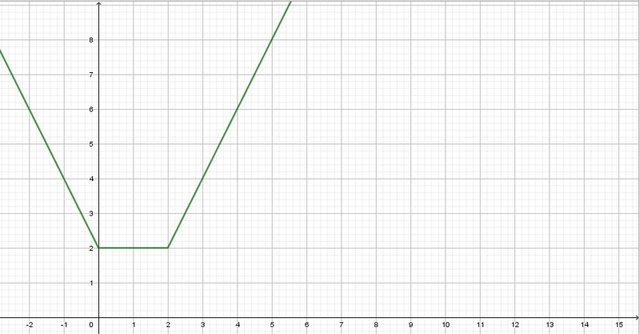
Построим функцию y = |x-2| + |x|.
После раскрытия модулей имеем, что:
1) На промежутке x≤0 есть функция y=-2x+2.
2) На промежутке 0< x ≤ 2 есть функция y = 2
3) На промежутке x>2 есть функция 2x-2
Рассмотрим теперь функцию f(x) = ax + 2(a-1). - линейная функция(графиком функции является прямая).
Из условия параллельности прямых очевидно, что при а = 2 функция f(x) || y = 2x-2 и меняя параметр а линейной функции при a ∈ [2;+∞), то имеем что уравнение имеет ровно одно решение.
Аналогично, линейная функция будет параллелен прямой у = -2х + 2 при a=-2 и в зависимости изменения параметра а имеем что при a ∈ (-∞;-2) уравнение будет иметь ровно один корень.
Если х = 2 и у = 2, то мы получим параметр a=1
 - ответ
- ответ