В основании прямой призмы лежит треугольник со сторонами 3 см и 5 см и углом между ними...

Question

В основании прямой призмы лежит треугольник со сторонами 3 см и 5 см и углом между ними 120 градусов. Боковое ребро 7 см. Найти площадь полной поверхности призмы.

Comments

Пожалуйста, можете написать больше объяснений.

Answer 1

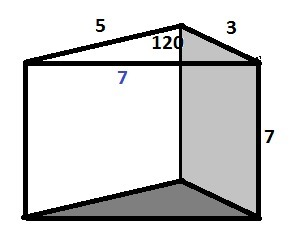
Третья сторона треугольника по т. Пифагора
с² = a² - b² + 2*a*b*cos 120°
cos 120° = - 0.5 
c² = 49,   
c = √49 = c.
Периметр основания
p = a+b+c = 3+5+7 =15 см
Площадь боковой поверхности
S,бок = p*h = 7*7 = 49 см² - боковая
Площадь основания по формуле Герона

где p = 1/2*(a+b+c) -  полупериметр.
Sосн = √(7,5 * 4,5*2,5*0,5) = √42,1875 ≈6,4952 - одно основание
Sполн = 49 + 12,99 = 61,99 ≈ 62  см²  - ОТВЕТ

---

Comments

А моё решение такое: 1) S осн.=1/2 a*b*sin 120 = 1/2*3*5*0.9 = 13,5см^2. 2) AB^2=AC^2+BC^2=9+25=в корне 34 = 5,8 см - AB. 3) S бок.= P осн.*H. 4) P осн.= AB+BC+AC=5,8+5+3=13,8 см. 5) S бок.= 13,8*7= 96,6 см^2. 6) S полн. = 96,6+2*13,5=123,6 см^2. Вот так или лучше как у тебя?