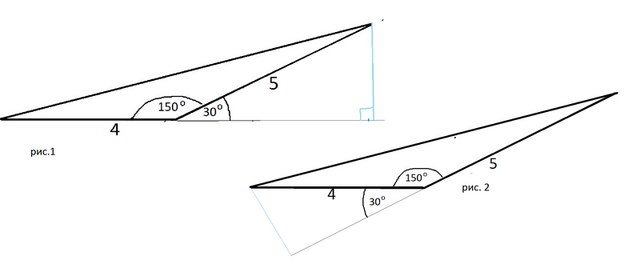
Треугольник дан тупоугольный, поэтому его высоты из вершин острых углов будут вне треугольника.
Продлим основание треугольника.
Опустим к нему высоту из вершины, лежащей против основания.
Эта высота противолежит углу 30° ( разность между развернутым углом и углом между сторонами треугольника)
Поэтому высота треугольника, опущенная из острого угла, равна половине стороны ( являющейся в этом прямоугольном треугольнике гипотенузой)
Имеется высота треугольника и основание, к которому она опущена.
На рисунке 1 в приложении гипотенузой получившегося прямоугольного треугольника стала сторона, равная 5 см.
Поэтому высота равна 5*sin(30°)=2,5 см
S=2,5*4:2=5 см²
С тем же результатом можно провести высоту к стороне, равной 5, и получим высоту, равную 2 см (см. рис.2)
S=2 *5:2=5 см²