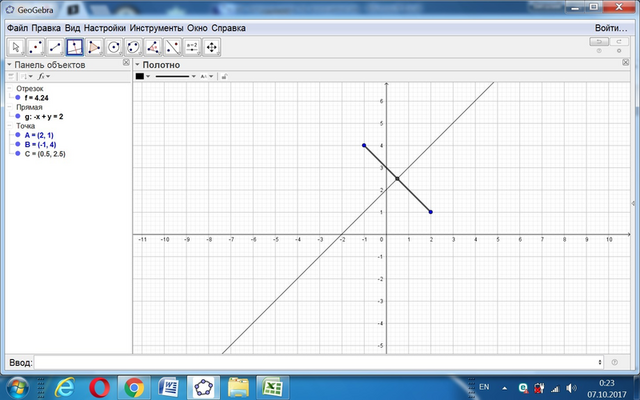
Геометрическое место точек, одинаково удаленных от двух точек A(2;1) и B(−1;4), - это прямая, перпендикулярная отрезку АВ и проходящая через его середину.
АВ: (х - 2)/(-1 - 2) = (у - 1)/(4 - 1).
АВ: (х - 2)/(-3) = (у - 1)/(3).
Это же уравнение в виде с коэффициентом:
у = -х + 3.
Находим координаты середины АВ - пусть это точка С.
С((2-1)/2=0,5; (1+4)/2=2,5) = (0,5; 2,5).
Уравнение искомой прямой: у = (-1/(-1))х + в = х + в.
Для определения коэффициента в в уравнение подставим координаты точки С: 2,5 = 0,5 + в, в = 2,5 - 0,5 = 2.
Ответ: у = х + 2.