Сразу про наибольшую площадь - она у квадрата - аксиома - без доказательства.
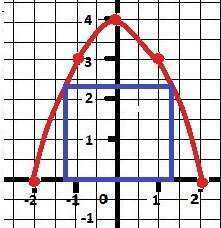
Делаем рисунок - график функции
Y = - x² + 4 - парабола, ветви вниз, вершина в точке (0;4)
Рисунок - в приложении.
Из него следует, что у вершины квадрат координата - y = 2*х.
Далее - подставим в уравнение функции.
2*x = -x² + 4
Переписали в удобный вид и получили квадратное уравнение.
- x²- 2x + 4 = 0
Решили и нашли
D= 20 и х1 = 1,236
Сторона квадрата - a = 2*х = 2.472
И площадь
S = a² ≈ 6.11 - ОТВЕТ
Числа не очень красивые, но правильные.