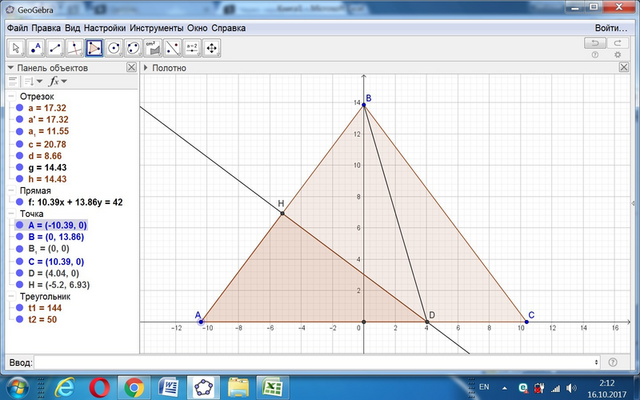
Имеем равнобедренный треугольник АВС, АВ = ВС. Точка Н - середина АВ. Перпендикуляр к АВ в точке Н - отрезок ДН. Площадь АВС = 144, площадь АНД = 50, угол ВАС = углу ВСА. Основание высоты из вершины В - точка Е.
Так как АН = НВ, НД ⊥ АВ, то треугольник АВД -равнобедренный. Угол ВАД = углу АВД.
Отсюда делаем вывод, что треугольники ВДА и АВС подобны по двум углам.
Площадь треугольника ВДА = 2*50 = 100.
Площади подобных треугольников относятся как квадрат коэффициента "к" подобия.
к = √(144/100) = √1,44 = 1,2.
Рассмотрим половины подобных треугольников - прямоугольные треугольники ВДН и АВЕ.
В треугольнике ВДН примем ВН = х, ДН = у, так как АВ = 2х, то ВД = (2х/1,2).
В треугольнике АВЕ катет АЕ = 1,2х, катет ВЕ = 1,2у, гипотенуза АВ = 2х.
Из него по Пифагору определяем:
ВЕ² = (2х)² - (1,2х)² = 4х² - 1,44х² =2,56х².
Тогда ВЕ = 1,2у = 1,6х.
Площадь АВЕ = 144/2 = 72.
Получаем 72 = (1/2)*АЕ*ВЕ = (1/2)*1,2х*1,6х = 0,96х².
х² = 72/0,96 = 75.
х = √75 = 5√3.
Ответ: боковые стороны равны по 2х = 2*5√3 = 10√3 кв.ед.