Биссектриса внешнего угла при вершине А треугольника АВС пересекает прямую ВС в точке Д....

Без проблем
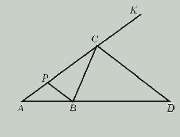
1) BP || CD
2) △APB ∾ △ACD; AC : PC = AD : BD
3) ∠BPC = ∠DCK соответственные при параллельных прямых; ∠PBC = ∠BCD внутренние накрест лежащие; ∠BCD = ∠DCK по условию задачи. ∠CPB = ∠PBC ; △CPB – равнобедренный, т. е. PC = CB.
AD : BD = AC : BC, ДОКАЗАНО!