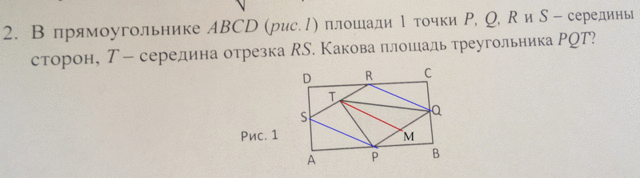
В прямоугольнике ABCD площади 1 точки P, Q, R и S - середины сторон, T - середина отрезка RS. Какова площадь треугольника PQT? (рисунок ниже)
Дано:
АВCD - прямоугольник
DR=RC=AP=PB
AS=SD=CQ=QB
ST=TR
S прямоугольника ABCD = 1
Найти S∆PQT
Решение:
1)Пусть а - длина прямоугольника
b - ширина его
ab = S
ab = 1
2)Соединим последовательно середины сторон P, Q, R, S и получим 4 равных треугольника ∆SDR = ∆RCQ = ∆QBP = ∆ASP (по двум равным сторонам и прямому углу между ними)
Найдём общую площадь этих треугольников.
S₁ = 4*1/2 *а/2 *в/2=ав/2 = 1/2
3)Из равенства треугольников ∆SDR = ∆RCQ = ∆QBP = ∆ASP следует равенство сторон SR=RQ=QP=PS.
Значит, SPQR - ромб.
Теперь найдём площадь ромба SPQR, для этого от площади всего прямоугольника 1 отнимем сумарную площадь угловых треугольников 1/2.
1 - 1/2 = 1/2
4) В ромбе через точку проведём прямую TM║PS и QR - сторонам ромба.
Получим 4 равных треугольника ∆PST=∆MPT=∆QMT=∆QTR(по трём равным сторонам).
5) 1/2 : 4 = 1/8 - площадь каждого из этих треугольников.
6) И, наконец, найдём площадь ∆PQT, который состоит из двух треугольников площадью по 1/8.
2 * 1/8 = 2/8 = 1/4
Ответ: S = 1/4