Cos2x=1-2sin²x
cos²2x=(1-2sin²x)²=(2sin²x-1)²
Значит уравнение имеет вид
sinx·(2sin²x-1)+(2sin²x-1)²=0
(2sin²x-1)(sinx+2sin²x-1)=0
Произведение двух множителей равно 0, когда хотя бы один из них равен 0 ( а другой при этом не теряет смысла, но в данном задании оба множителя определены при любых х и потому никаких проблем).
1)
2sin²x-1=0 ⇒ sinx=-√2/2 или sinx=√2/2
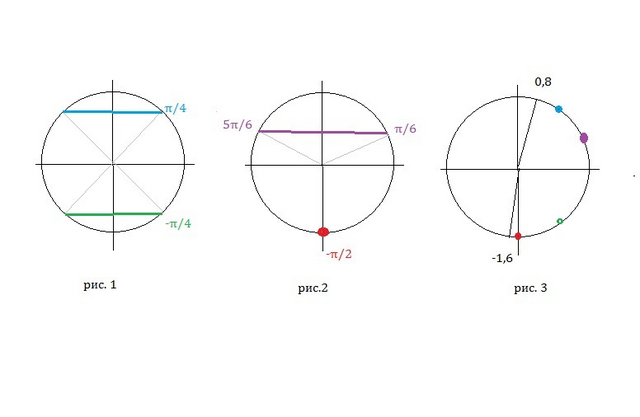
х=(π/4)+(π/2)k, k∈ Z ( cм рис.1)
2)2sin²x+sinx-1=0
D=1-4·2·(-1)=9
sinx=-1 или sinx=1/2
x=(-π/2)+2πm, m∈z или х=(π/6)+2πn, n∈Z или х=(5π/6)+2πr, r∈Z
(cм. рис.2)
О т в е т. (π/4)+(π/2)k;(-π/2)+2πm;(π/6)+2πn;(5π/6)+2πr, k,m,n, r∈Z
б) Указанному отрезку принадлежат корни ( cм. рис.3)
-π/2≈-1,57
-π/4≈-0,785
π/6≈0,522
π/4≈0,785