III.
1. Дана произвольная треугольная призма АВСА1В1С1.
Точки K, N, M - принадлежат ребрам АА1, АС и А1В1 соответственно.
Найти сечение KNM.
решение:
Точки К и М принадлежат одной грани АА1В1В, следовательно МК - линия пересечения секущей плоскости и этой грани. Если продлить эту линию до пересечения с продолжением ребра ВА, то получим точку 1, принадлежащую и секущей плоскости (прямой МК) и грани АВС (прямая ВА принадлежит плоскости АВС). Тогда, проведя через точки 1 и N прямую до пересечения с ребром ВС, получим точку Н, принадлежащую и плоскости сечения, и грани ВВ1С1С. Если продолжим прямую ВВ1 до пересечения с прямой КМ (ее продолжением), то получим точку 2, принадлежащую и секущей плоскости (прямой КМ) и грани ВВ1С1С. Тогда, проведя через точки 2 и Н прямую до пересечения с ребром В1С1, получим точку Р, принадлежащую и плоскости сечения, и грани ВВ1С1С.
Соединив точки N,K,M,P,H и N, получим искомое сечение NKMPH.
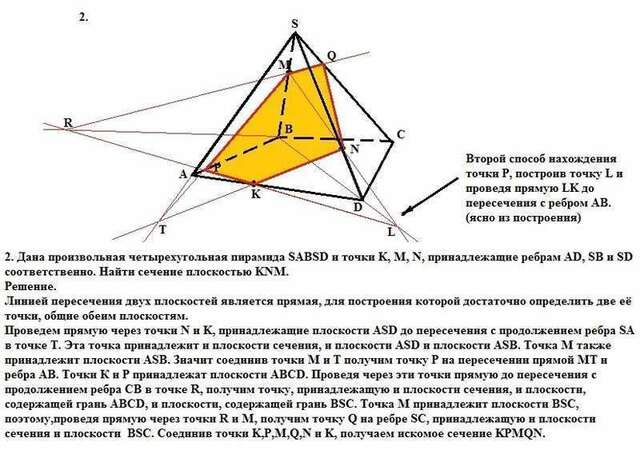
2. Дана произвольная четырехугольная пирамида SABSD и точки K, M, N, принадлежащие ребрам AD, SB и SD соответственно. Найти сечение плоскостью KNM.
Решение.
Линией пересечения двух плоскостей является прямая, для построения которой достаточно определить две её точки, общие обеим плоскостям.
Проведем прямую через точки N и K, принадлежащие плоскости ASD до пересечения с продолжением ребра SA в точке Т. Эта точка принадлежит и плоскости сечения, и плоскости ASD и плоскости ASB. Точка М также принадлежит плоскости ASB. Значит соединив точки М и Т получим точку Р на пересечении прямой МТ и ребра АВ. Точки К и Р принадлежат плоскости АВСD. Проведя через эти точки прямую до пересечения с продолжением ребра СВ в точке R, получим точку, принадлежащую и плоскости сечения, и плоскости, содержащей грань ABCD, и плоскости, содержащей грань BSC. Точка М принадлежит плоскости ВSC, поэтому,проведя прямую через точки R и М, получим точку Q на ребре SC, принадлежащую и плоскости сечения и плоскости BSC. Соединив точки K,P,M,Q,N и K, получаем искомое сечение KPMQN.
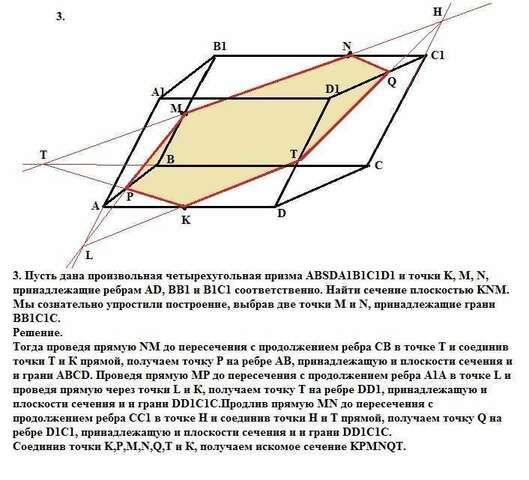
3. Пусть дана произвольная четырехугольная призма ABSDA1B1C1D1 и точки K, M, N, принадлежащие ребрам AD, ВB1 и В1С1 соответственно. Найти сечение плоскостью KNM.
Мы сознательно упростили построение, выбрав две точки M и N, принадлежащие грани ВВ1С1С.
Решение.
Тогда проведя прямую NM до пересечения с продолжением ребра СВ в точке Т и соединив точки Т и К прямой, получаем точку Р на ребре АВ, принадлежащую и плоскости сечения и и грани АВСD. Проведя прямую MР до пересечения с продолжением ребра А1А в точке L и проведя прямую через точки L и К, получаем точку Т на ребре DD1, принадлежащую и плоскости сечения и и грани DD1C1C.Продлив прямую МN до пересечения с продолжением ребра СС1 в точке Н и соединив точки Н и Т прямой, получаем точку Q на ребре D1C1, принадлежащую и плоскости сечения и и грани DD1C1C.
Соединив точки K,P,M,N,Q,T и К, получаем искомое сечение KPMNQT.