В параллелограмме ABCD высота, опущенная ** сторону CD, делит её пополам и образует со...

Question

В параллелограмме ABCD высота, опущенная на сторону CD, делит её пополам и образует со стороной BC угол 30 градусов, AB=12 см .найдите периметр параллелограмма

Answer 1

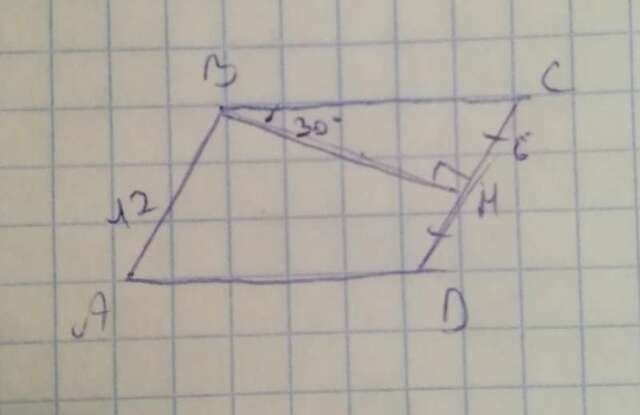
AB = CD = 12 см (по свойству параллелограмма) 
т.к. BH - высота, делит CD пополам, следовательно CH и HD = 6 cм.
Треугольник BHC - прямоугольный, т.к. угол BHC = 90 градусов, BC - гипотенуза. 
Т.к. угол B = 30 градусам, следовательно CH = 1/2 BC ( по углу в 30 градусов и противолежащему катету) 
6 = BC/2 следовательно BC = 6*2 = 12 
P - периметр = AB + BC + CD + AD 
P = 12 + 12 + 12 + 12 = 48 см

---