Теорема Фалеса:
Если на одной из двух прямых отложить последовательно равные отрезки и через их концы провести параллельные прямые, пересекающие вторую прямую, то они отсекут на второй прямой равные между собой отрезки.
По условию четыре данные прямые параллельны, отсекают на прямой ЕН отрезки, равные длине отрезка ЕF, т.е. 6 см.
Значит, ЕН=3•6=18 см
CD=CB=AB=4, и AD=3•4=12 см
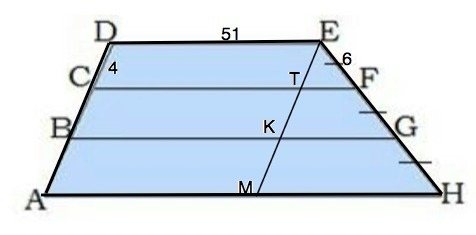
Проведем параллельно AD прямую ЕМ, пересекающую параллельные прямые СF и BG в точках Т и К соответственно.
СТ=ВК=АМ=DE=51 см.
ТF=CF-51=57-51=6 см,
∆ МЕН параллельные прямые делят на подобные ∆ ТЕF; ∆ KEG;
TF - средняя линия ∆ КЕG⇒ KG=2•TF=12
BG=51+12=63
КT=КМ=ТЕ=4
У подобных ∆TEF k=EH:EF=18:6=3⇒
MH=6•3=18 см
Итак, АD=3•4=12,
EH=18
DF=51; CF=57
AH=51+18=69
Необходимо 12+18+57+63+69+51=30+120+120=270 м прута.