В треугольнике ABC известно, что AB=2, BC=4, AC=3, BN - биссектриса треугольника. Прямая,...

Question

В треугольнике ABC известно, что AB=2, BC=4, AC=3, BN - биссектриса треугольника. Прямая, проходящая через вершину A перпендикулярно BN, пересекает сторону BC в точке M. Докажите, что биссектриса угла С делит пополам отрезок MN.

Answer 1

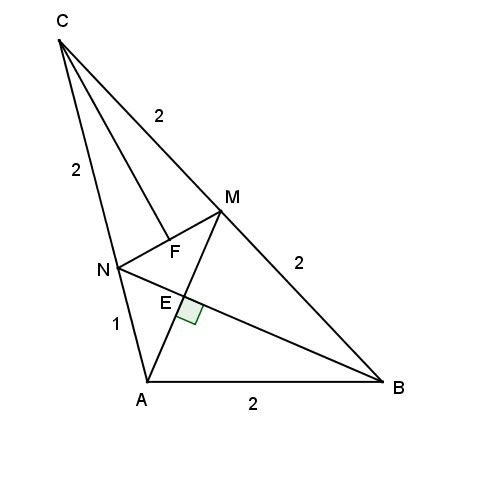
Пусть Е - точка пересечения MA и BN. Тогда треугольник MAB - равнобедренный (его биссектриса BE по условию является и его высотой), т.е. BM=AB=2, откуда CM=BC-BM=4-2=2. Т.к. BN - биссектриса треугольника ABC, то CN/NA=BC/AB=4/2=2, т.е. CN=2/3·AC=2/3·3=2. Итак, CM=CN=2, т.е. треугольник NCM - равнобедренный, и значит, его биссектриса CF является одновременно и медианой, что и требовалось.

---