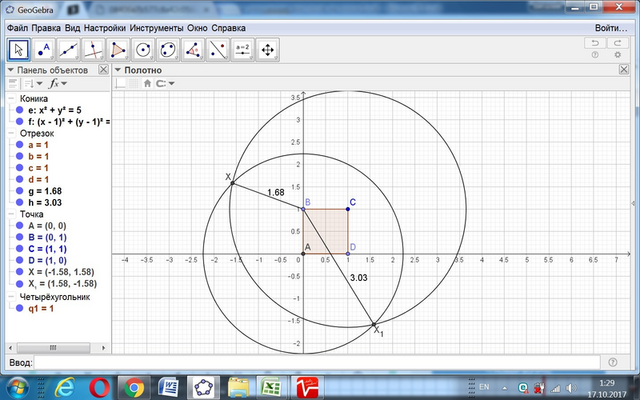
ГМТ, удалённых от заданной точки на заданное расстояние - это окружность с радиусом, равным заданному расстоянию.
Координаты точки Х находим совместным решением уравнений таких окружностей.
Поместим квадрат АВСД в прямоугольную систему координат точкой А в начало, стороной АД по оси Ох.
Точка А (0; 0), точка С (1; 1).
Уравнение окружности с центром в точке А:
х² + у² = 5.
Уравнение окружности с центром в точке С:
(х - 1)² + (у - 1)² = 7.
Решаем систему:

Раскроем скобки:

Подставим вместо х² + у² число 5 и получим:
-2х - 2у = 0 или у = - х.
Это говорит о том, что точка Х лежит на прямой у = -х.
Подставим это свойство в первое уравнение:
х² + (-х)² = 5,
2х² = 5,
х = +-√(5/2) ≈ +-
1,5811388. Тогда у = -+1,5811388.
Имеем две точки, где может находиться точка Х:
Х((-√(5/2)); √(5/2)) и Х₁((√(5/2)); -√(5/2)).
Имеем и 2 расстояния от точки Х до точки В.
Расстояние между точками.
d
= √((х2 - х1)² + (у2 - у1 )²).
BХ = 1,684554,
BХ1 = 3,026925.