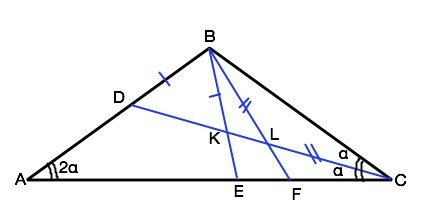
В треугольнике АВС CD –биссектриса угла АСВ, АВ=ВС, BD=BK, BL=CL. Докажите, что BF– биссектриса угла СВЕ.
----------
В равнобедренном треугольнике АВС отрезок СД, ⇒ ∠DСВ=∠DСА. Примем угол DСВ равным α.
Тогда в ∆ АВС ∠ВАС=∠ВСА=2 α
Угол АВС=180°-(угол А+угол С)=180°-4α
∠KLB - внешний для ∆ ВLC и равен сумме внутренних углов - равен 2α
∠ВDС=180°- (∠DВС+∠DСВ)=180° -(180-4α+α)=3α
В равнобедренном ∆ КВD угол ВКD=углу ВDК=3α
∠ВКД - внешний для ∆ ВКL и равен сумме его внутренних углов ⇒
КВL+BLK=3 α ⇒
∠KВL=3α-угол KLB=3α-2α=α, из чего следует равенство углов FВЕ=FВС.
Следовательно. ВF делит угол СВЕ пополам и является биссектрисой угла СВЕ.