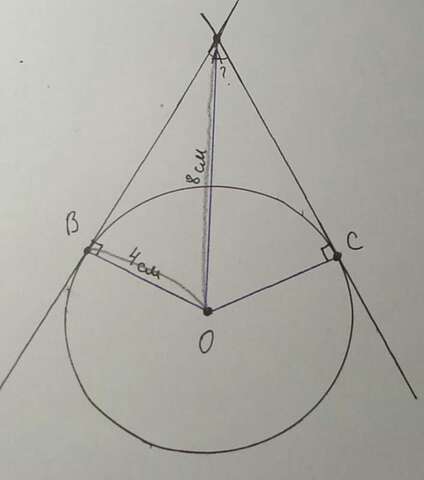
Дано:
Окружность (О, R);
АВ;АС - касательные;
АВ пересекает АС = А;
ОВ = ОС - радиусы;
ОВ = 4 см;
ОА = 8 см.
—————
Найти: угол ВАС
Решение:
Касательная к окружности перпендикулярно радиусу, проведенному в точку касания => угол ОВА = углу ОСА = 90°;
Рассмотрим ∆ОВА:
ОВ - катет (=4 см)
ОА - гипотенуза (= 8 см)
ОА = 2ОВ => катет прямоугольного треугольника, равный половине гипотенузе, лежит против угла в 30° => угол ВАО = 30°
Отрезки касательных к окружности, проведенные из одной точки, равны и составляют равные углы с прямой, проходящей через эту точку и центр окружности, т.е. угол ВАО = углу ОАС = 30°
Угол ВАС = 30×2= 60°
Ответ: угол ВАС = 60°