5/Задание №
5:
Ваня моложе своего отца на 32 года, а его отец на столько же
моложе своего отца - дедушки Вани. Всем им вместе не более ста лет, и всем
целое число лет. Сколько лет было дедушке Вани пять лет назад?
РЕШЕНИЕ: Пусть дедушке х лет. Тогда, папе (х-32) лет, а Ване
- (х-32-32)=(х-64) лет.
Сумма возрастов: х+х-32+х-64=3х-96
3х-96<=100</p>
3х<=196</p>
x<=65+1/3</p>
Максимально возможное значение х=65, при этом папе 65-32=33
года. а Ване 33-32=1 год.
Если х=64 или меньше, то Ване 0 или менее лет - не может
быть.
Дедушке Вани пять лет назад было 65-5=60 лет
ОТВЕТ: 60 лет
5/Задание №
6:
Отрезок, равный 36 см, разделён на четыре неравных отрезка.
Расстояние между серединами крайних отрезков равно 26 см. Найдите расстояние
между серединами средних отрезков. Дайте ответ в сантиметрах.
РЕШЕНИЕ: Пусть длины отрезков равны a, b, с, d. Тогда:
Длина всего отрезка: а+b+с+d=36.
Расстояние между серединами крайних отрезков включает
половины длин крайних и длины двух средних а/2+b+с+d/2=26.
Второе уравнение умножаем на 2: а+2b+2с+d=52.
Из получившегося уравнения вычитаем первое: b+c=16.
Если разделить уравнение на 2, то получится расстояние между
серединами средних отрезков: b/2+c/2=8.
ОТВЕТ: 8 см
5/Задание №
7:
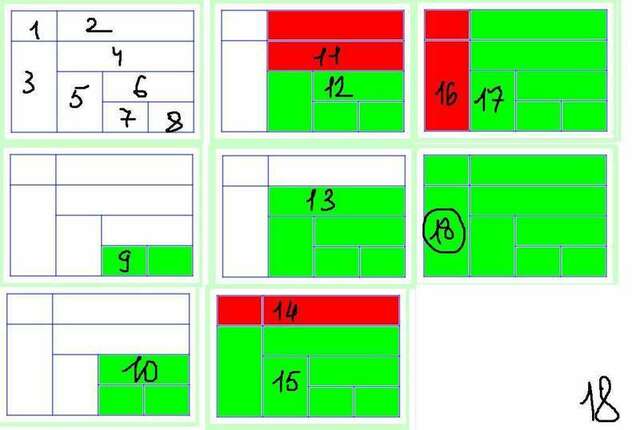
Сколько прямоугольников можно найти на картинке?
РЕШЕНИЕ: нумерация на рисунке
ОТВЕТ: 18 прямоугольников